Welcome to UNIZOR.COM [ Ссылка ].
Theorem 1
Given two chords of equal length crossing each other in the same circle and divided by a point of intersection in two unequal segments each, short and long. Prove that a short segment of one chord is congruent to a short segment of another and, similarly, a long segment of one is congruent of a long segment of another.
Theorem 2
Two circles intersect at points A and B. A secant is drawn through point A intersecting circles at points C and D. Prove that the measure of angle ?CBD does not depend on position of secant CD as long as it goes through point A.
Theorem 3
Two circles with centers in points K and L are tangent to each other at point M. Two secants, intersecting both circles, are drawn: one from point A in the first circle through M to point B in the second circle; another from point C in the first circle through M to point D in the second circle. Prove that chords AC in the first circle and BD in the second circle are parallel to each other.
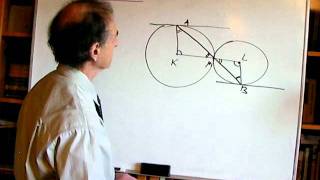
Theorem 4
Two circles with centers in points K and L are tangent to each other at point M. A secant, intersecting both circles, is drawn from point A in the first circle through M to point B in the second circle. Prove that a tangent to the first circle at points A and a tangent to the second circle at point B are parallel to each other.
Theorem 5
If in any triangle bases of three altitudes are connected to form a new triangle, then these altitudes will be angle bisectors in a new triangle.
Theorem 6
Given an equilateral triangle ?ABC inscribed into a circle. For any point M on a circle, connected to all three vertices of this triangle, sum of the lengths of two shorter connections to vertices equals to the length of the longer one.

свернуть