Paper link: [ Ссылка ]
In this paper, we present a convex optimization
problem to generate Center of Mass (CoM) and momentum
trajectories of a walking robot, such that the motion robustly
satisfies the friction cone constraints on uneven terrain. We
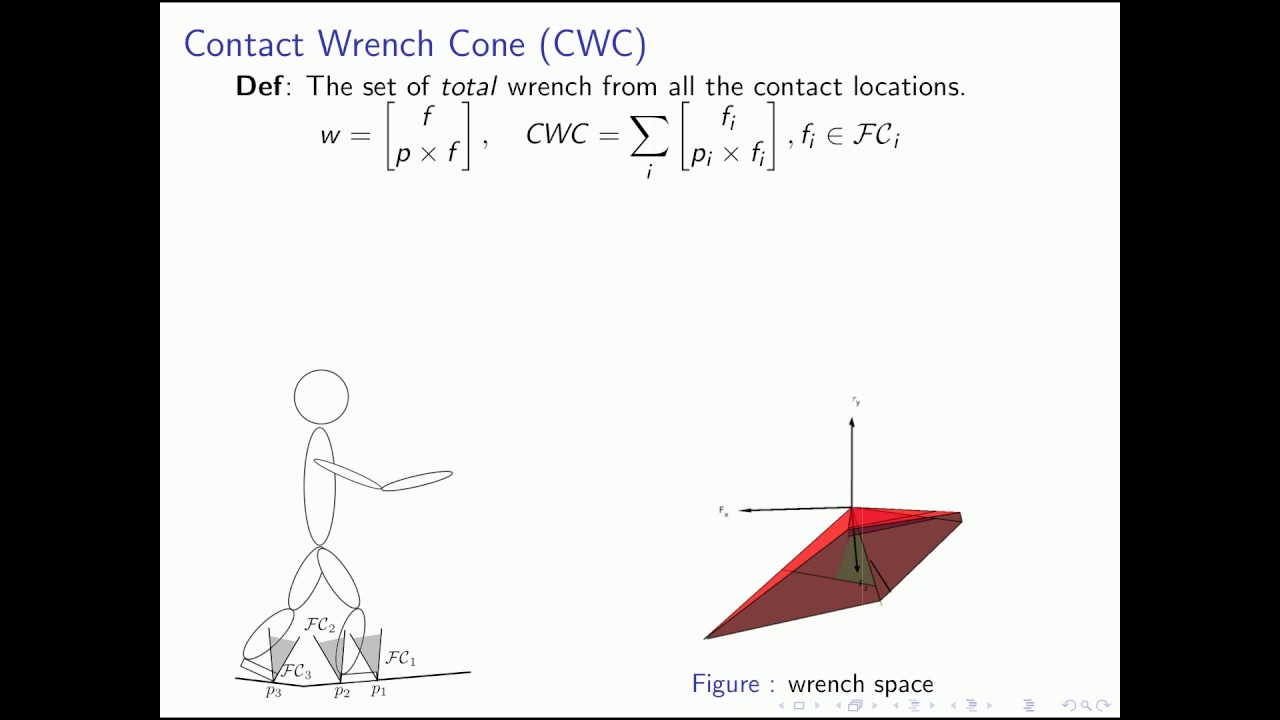
adopt the Contact Wrench Cone (CWC) criterion to measure
a robot’s dynamical stability, which generalizes the venerable
Zero Moment Point (ZMP) criterion. Unlike the ZMP criterion,
which is ideal for walking on flat ground with unbounded
tangential friction forces, the CWC criterion incorporates noncoplanar
contacts with friction cone constraints. We measure
the robustness of the motion using the margin in the Contact
Wrench Cone at each time instance, which quantifies the capability
of the robot to instantaneously resist external force/torque
disturbance, without causing the foot to tip over or slide. For
pre-specified footstep location and time, we formulate a convex
optimization problem to search for robot linear and angular
momenta that satisfy the CWC criterion. We aim to maximize
the CWC margin to improve the robustness of the motion, and
minimize the centroidal angular momentum (angular momentum
about CoM) to make the motion natural. Instead of directly
minimizing the non-convex centroidal angular momentum, we
resort to minimizing a convex upper bound. We show that our
CWC planner can generate motion similar to the result of the
ZMP planner on flat ground with sufficient friction. Moreover,
on an uneven terrain course with friction cone constraints, our
CWC planner can still find feasible motion, while the outcome
of the ZMP planner violates the friction limit.