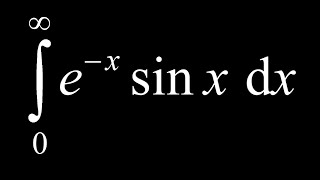To find the definite integral of e^-x*sin(x) on zero to infinity, we have to use the integration by parts loop trick, in which we apply integration by parts twice in search of a copy of the original integral on the right hand side. This time, we use two iterations of integration by parts with an infinite limit, but we handle the limit at infinity informally by using the fact that e^-infinity is unambiguously zero.
We start with the first iteration of integration by parts and say let u=e^-x and dv=sin(x)dx. We use the integration by parts formula to obtain the result, which gives us -e^-x*cos(x) -integral(e^-x*cos(x)dx). This is a definite integral with integration by parts, so we evaluate the first term across the limits of integration, giving us 1. The evaluation requires subbing infinity into e^-x*cos(x), but e^-infinity is zero and cos(x) is bounded between -1 and 1. Zero multiplied by a finite number gives us zero, so that term vanishes. Subbing in the lower limit gives us 1.
Now we apply integration by parts for the second time, letting u=e^-x (the same part of the integral we called u the first time) and dv=cos(x)dx. Applying the integration by parts formula, we get another term to be evaluated from zero to infinity (e^-x*sin(x)) in addition to a copy of the original integral! When we sub the upper and lower limits into e^-x*sin(x), we obtain zero for each limit, the our right hand side is now just one minus the original integral.
Now we can gather both copies of the original integral to the left hand side and divide by 2 to obtain the final result for the integral of e^-x*sin(x) on zero to infinity: 1/2.