In this video we cover how to conduct hypothesis testing the difference between 2 proportions, or how to do a two sample z-test. We go through the formula used and the steps, using an example problem and working through it.
Transcript/notes (partial)
In hypothesis testing the difference between population proportions p1 and p2, we use samples to calculate a standardized test statistic and reject or fail to reject a null hypothesis depending on whether that test statistic falls in a rejection region.
The usual pairing of hypotheses are listed here, and we always assume there is no difference between the population proportions, so p1 = p2.
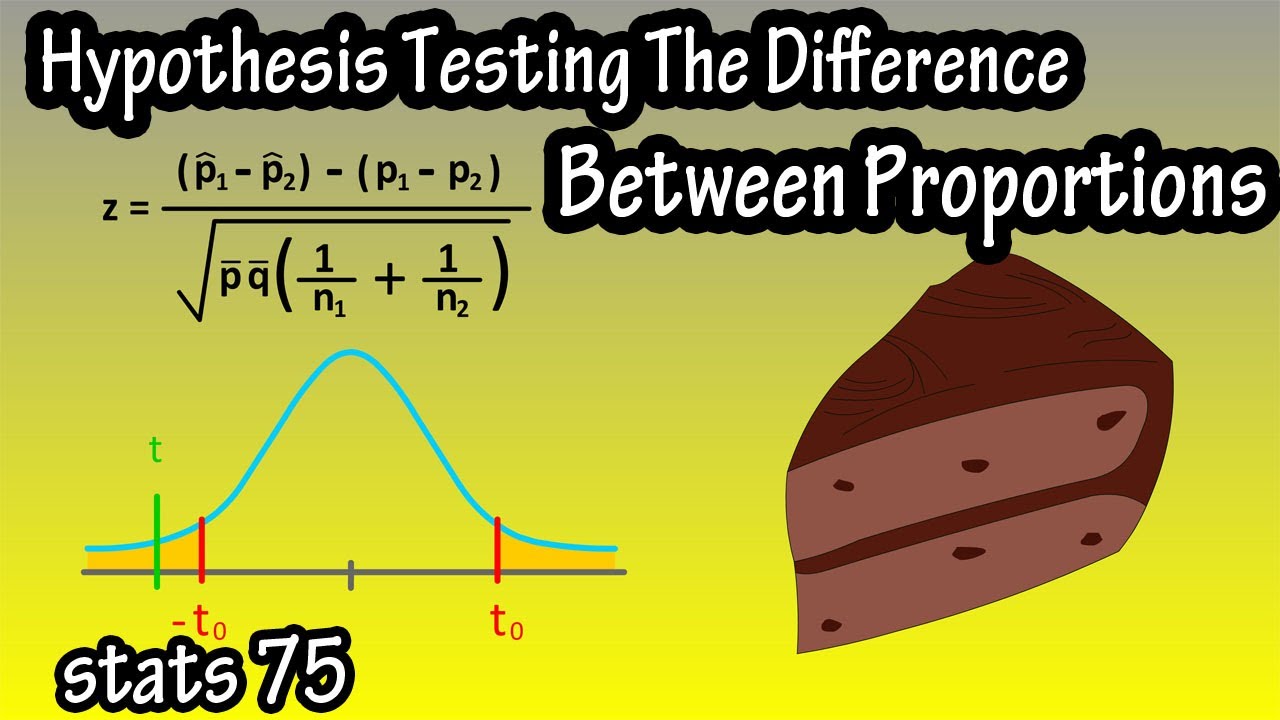
And, the formula for calculating the standardized test statistic is z equals phat1 minus phat2 minus p1 minus p2 divided by the square root of pbar times qbar times 1 over n1 plus 1 over n2.
In this formula, z is the standardized test statistic, phat1 is the proportion for sample 1, phat2 is the proportion for sample 2, p1 and p2 are the population proportions, which we always assume are equal.
Pbar is a weighted estimate of p1 and p2. The formula for pbar is n1 times phat1 plus n2 times phat2 divided by n1 plus n2. And this formula is often times shortened to pbar equals x1 plus x2 divided by n1 plus n2.
As an example, if I said in a random sample of 122 people, 44 of them were wearing a necklace, the sample proportion would be 44 divided by 122, which is 0.361, so x = 44, n = 122, and p hat = 0.361.
Now, in the conditions, for number 3, it is going to be n1pbar, n1 qbar, n2pbar, and n2qbar must all be greater than or equal to 5
Alright, let’s go through a full example step by step.
A recent study of 132 randomly selected females and 120 males showed 33% of females and 45% of males had a dessert after dinner. At a level of significance of 0.10, can you reject the claim that the proportion of people who eat dessert after dinner is the same for females and males.
Step 1 is to make sure the first 2 conditions are met. And it is a random sample, and the samples are independent, females and males.
Step 2 is to find the weighted estimate of p1 and p2, find pbar. We first need to calculate x1 and x2, which I have done here, then we plug those into our pbar formula and get approximately 0.3889. And for qbar we get approximately 0.6111.
Step 3 is to make sure condition 3 is met, which I have done here, so this condition is met.
Step 4 is to write the claim out and identify the null and alternative hypotheses. The claim is that the proportion of people who eat dessert after dinner is the same for females and males. So, the claim is that p1 equals p2. And we know the null hypothesis contains a statement of equality, so h sub 0 is p1 = p2. The alternative hypothesis is the complement of the null hypothesis and contains a statement of inequality, so h sub a is p1 does not equal p2.
Step 5 is to identify the level of significance, which was given, alpha = 0.10.
Step 6, is to determine the test to use, left tailed, right tailed or 2 tailed, and because the alternative hypothesis contains the does not equals inequality, this will be a 2 tailed test.
Step 7 is to determine the critical values. Graphically this looks like this, with our critical values, negative z naught and positive z naught, here and the shaded areas in the tails being the rejection regions. Since the level of significance, alpha equals 0.10, and this is a 2 tailed test, the rejection regions will equal one half of alpha, which is 0.05. And in the z distribution table that value is -1.645 and positive 1.645, so those are our critical values.
Step 8 is to identify the rejection region, which is any standardized test statistic value that falls in the shaded area, that is any value that is less than -1.645 or greater than positive 1.645.
Step 9, use the formula and calculate the z value, or the value of the standardized test statistic. And in our example, we have 0.333 minus 0.45 minus 0, as we assume p1 minus p2 equals 0, divided by the square root of 0.3889 times 0.6111 times 1 over 132 plus 1 over 120. And this calculates out to -1.8974
Step 10 is to make a decision to reject or fail to reject the null hypothesis. On our graph, you can see that the standardized test statistic does fall in the rejection region to the left. So, in this case we would reject the null hypothesis.
Step 11 is to interpret the decision. There is enough evidence at the 10% level of significance to reject the claim that the proportion of people who eat dessert after dinner is the same for females and males.
Timestamps
0:00 Using Samples To Test Difference Between Population Proportions
0:25 Conditions To Use A Z Test
0:49 Formula For A Z Test For Testing The Difference Between Population Proportions
2:20 Example Problem Using A Z Test For Testing The Difference Between Population Proportions
3:56 Finding The Critical Values
4:26 Determining The Rejection Regions
4:38 Calculating The Z Value



























































![[4K] 피트니스 모델 '아사다 윤' 세로 직캠 @ 2023 WBFF](https://i.ytimg.com/vi/ikiWGurNmqY/mqdefault.jpg)