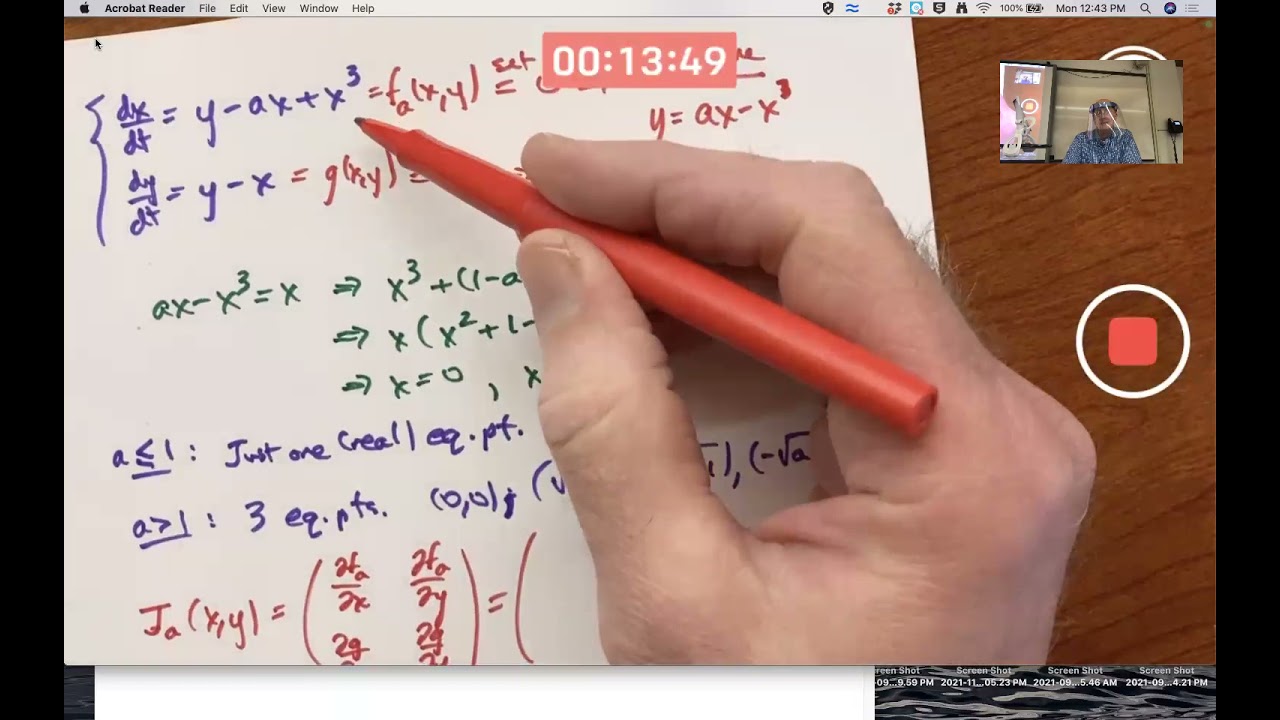
Find bifurcation values of the nonlinear system of differential equations x' = y - a*x + x^3, y' = y - x. Use linearization with the Jacobian matrix. Sketch the phase portrait when a = 2. Hamiltonian system x' = -2x*y - 1, y' = -3x^2 + y^2 with Hamiltonian function H(x,y) = x^3 - x*y^2 - y. Gradient system x' = 3x^2 - y, y' = -2x*y - 1 with potential function H(x,y) = x^3 - x*y^2 - y. Use ContourPlot on Mathematica for the level curves. Theorems about when an n x n matrix A is diagonalizable. Importance of diagonalization to linear systems of differential equations (matrix exponential) and linear systems of difference equations (matrix power). Orthogonal basis of a subspace W and orthogonal projections onto the subspace W (and the corresponding vector in the orthogonal complement of W).

[ Ссылка ]. (Differential Equations, 4th Edition (by Blanchard, Devaney, and Hall)). Amazon Prime Student 6-Month Trial: [ Ссылка ].

Links and resources
===============================
🔴 Subscribe to Bill Kinney Math: [ Ссылка ]
🔴 Subscribe to my Math Blog, Infinity is Really Big: [ Ссылка ]
🔴 Follow me on Twitter: [ Ссылка ]
🔴 Follow me on Instagram: [ Ссылка ]
🔴 You can support me by buying "Infinite Powers, How Calculus Reveals the Secrets of the Universe", by Steven Strogatz, or anything else you want to buy, starting from this link: [ Ссылка ].
🔴 Check out my artist son Tyler Kinney's website: [ Ссылка ]

⏱️TIMESTAMPS⏱️
(0:00) Class plan
(1:07) In-depth nonlinear system bifurcation problem (linearize with the Jacobian matrix and use the trace-determinant plane)
(29:02) Hamiltonian Systems and Gradient Systems
(45:51) Diagonalization facts and applications
(58:22) Projection vector onto a subspace when given an orthogonal basis of that subspace (also discuss orthogonal complement of a subspace)

AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.

свернуть