Perpendicular Bisector Theorem (Proof, Converse, & Examples)
Perpendicular
All good learning begins with vocabulary, so we will focus on the two important words of the theorem. Perpendicular means two line segments, rays, lines or any combination of those that meet at right angles. A line is perpendicular if it intersects another line and creates right angles.
Bisector
A bisector is an object (a line, a ray, or line segment) that cuts another object (an angle, a line segment) into two equal parts. A bisector cannot bisect a line, because by definition a line is infinite.
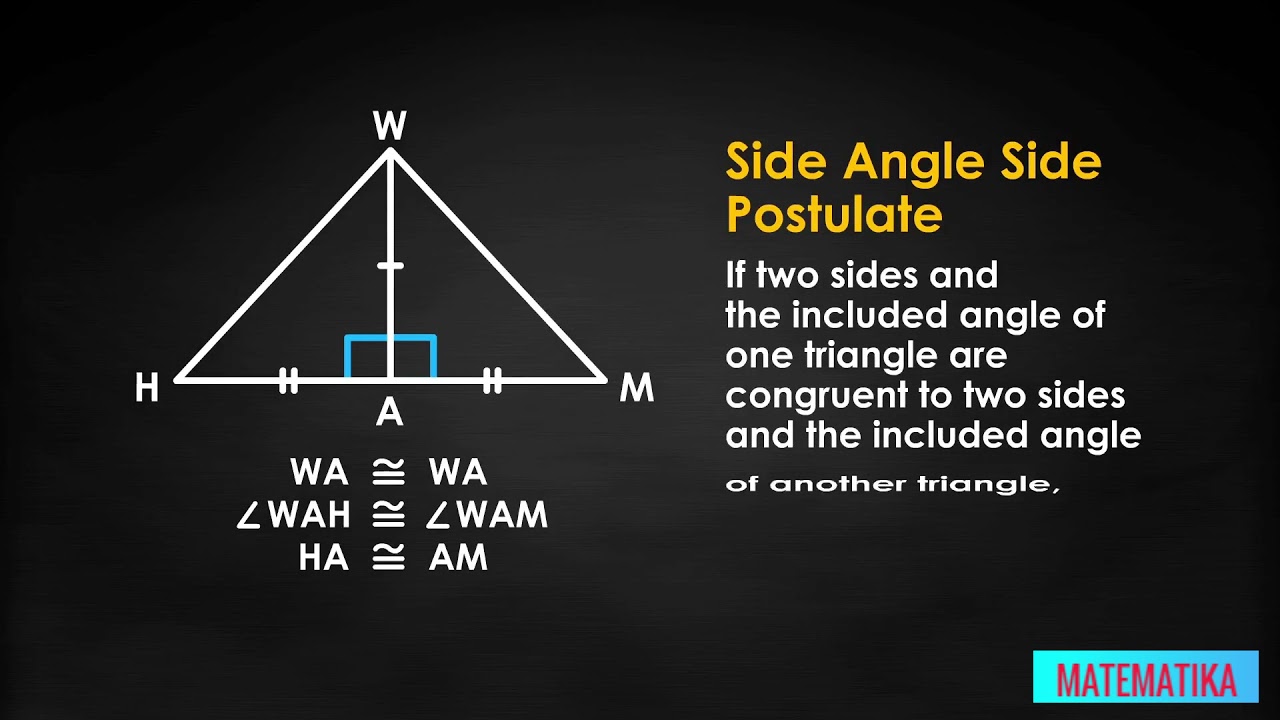
Perpendicular Bisector
Putting the two meanings together, we get the concept of a perpendicular bisector, a line, ray or line segment that bisects an angle or line segment at a right angle.
Video Summary
After you worked your way through all the angles, proofs and multimedia, you are now able to recall the Perpendicular Bisector Theorem and test the converse of the Theorem. You also got a refresher in what "perpendicular," "bisector," and "converse" mean.