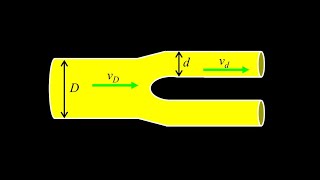
In this introductory fluid dynamics physics problem, we apply the fluid continuity equation for the flow of an incompressible fluid: we apply the continuity equation, which enforces that the same volume per unit time (the same flow rate) must occur at each point in a fluid system if the fluid is incompressible.

The complication in this problem is that the pipe splits into two pipes, so the flow rate in the two smaller pipes requires us to include a factor of two with the flow rate in one of the smaller pipes in order to express the total flow rate in that part of the system.

We start by expressing the flow rate in the large pipe using the flow rate equation f=Av, the product of cross sectional area and fluid speed. Then we express the flow rate in *one* of the smaller pipes using the same equation for the flow rate.

Next, the continuity equation simply says that the flow rate at each point in the system is the same. So, we set the flow rate in the large pipe equal to *twice* the flow rate in one of the smaller pipes, then we find the fluid speed in the smaller pipes in terms of the other parameters, and we're done!

свернуть