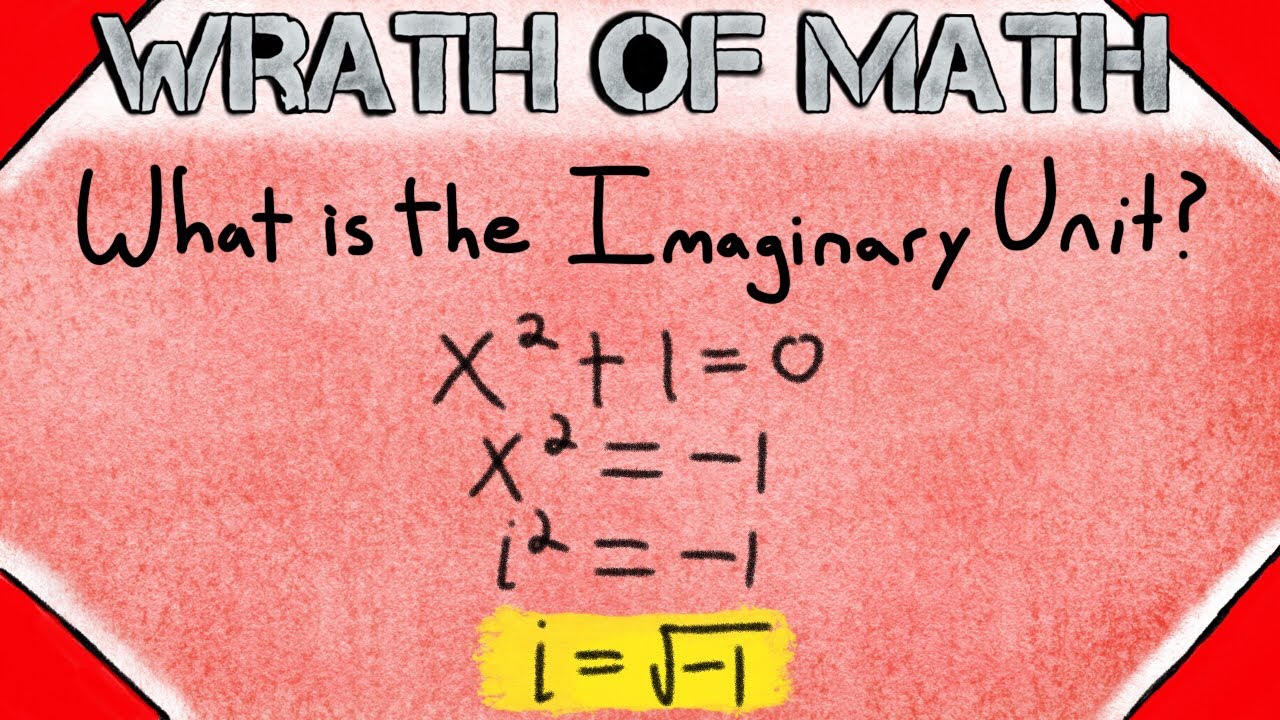What is the imaginary unit? The imaginary unit, i, is the topic of today's math lesson. The imaginary unit is defined as a solution to the equation x^2 + 1 = 0. This is equivalent to the equation x^2 = -1. Recall that any real number squared is positive, so there is no real number solution to the equation x^2 = -1. The imaginary unit is a solution that is not a real number. The imaginary unit, i, has the special property that its square is -1. So, i^2 = -1. Also, (-i)^2 = -1, because (-i)^2 = (-i)(-i) = (-1)(-1)(i)(i) = i^2 = -1.
Notice that we call i the imaginary unit, not -i. When we multiply i by real numbers like negative one, we get what are called imaginary numbers. Of course, i is also an imaginary number because it is the product of the real number one and i, but more specifically we call it the imaginary unit. Numbers like 5i, -3.2i, 4i, 2.65437i, are all imaginary numbers because they are real number multiples of the imaginary unit.
I hope you find this video helpful, and be sure to ask any questions down in the comments!
********************************************************************
The outro music is by a favorite musician of mine named Vallow, who, upon my request, kindly gave me permission to use his music in my outros. I usually put my own music in the outros, but I love Vallow's music, and wanted to share it with those of you watching. Please check out all of his wonderful work.
Vallow Bandcamp: [ Ссылка ]
Vallow Soundcloud: [ Ссылка ]
Vallow SoundCloud: [ Ссылка ]
********************************************************************
+WRATH OF MATH+
◆ Support Wrath of Math on Patreon: [ Ссылка ]
Follow Wrath of Math on...
● Instagram: [ Ссылка ]
● Facebook: [ Ссылка ]
● Twitter: [ Ссылка ]
Music Channel: [ Ссылка ]