KEYNOTE TALK - SIPS 2022, Trovalusci International Symposium

The role of plastic strain gradients on metallic fracture
Emilio Martinez-Paneda
Imperial College London

ABSTRACT
Macroscopic fracturing in metallic materials depends sensitively on properties that pertain to the micro and atomic scales. Durability predictions of engineering components require enriching continuum theories to properly characterize behaviour at the small scales involved in crack tip deformation. The deficiencies intrinsic to conventional plasticity motivate the development of mechanistically-based models. Namely, unrealistically low stresses are predicted ahead of the crack tip, with toughness being unbounded for cohesive strengths of approximately 3 times the yield stress in a perfectly plastic material ( σ_c/σ_Y→4 in a mild hardened solid). Tensile stresses on the order of 3-5 times the initial yield stress fail to explain decohesion at the atomic scale. Brittle fracture in the presence of significant plastic flow has been observed in numerous material systems; well-known examples include ferritic steels at low temperatures, hydrogen-embrittled metals or metal-ceramic interfaces. Since atomic separation requires traction levels on the order of the theoretical lattice strength (10σ_Y or larger), classic continuum theories would appear to rule out a fracture mechanism based on atomic decohesion whenever plasticity develops in the vicinity of the crack.
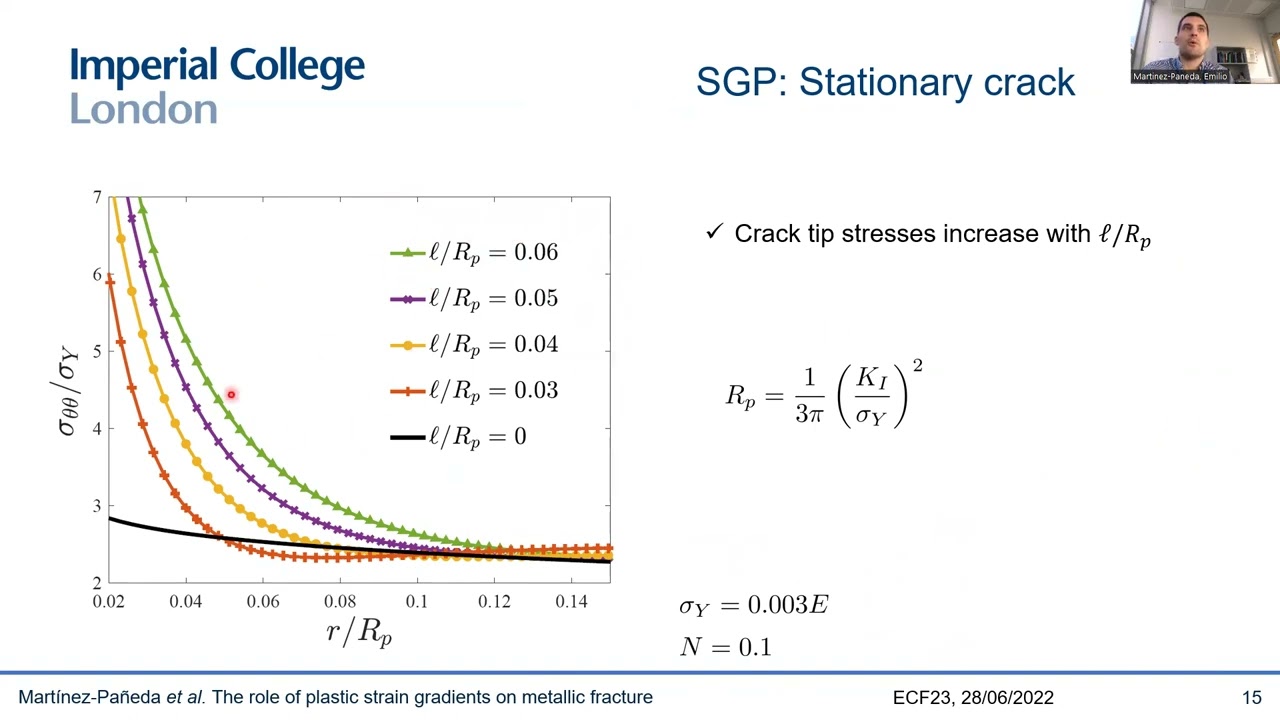
We investigate the implications of using strain gradient plasticity to provide a richer description of fracture in metallic materials. Strain gradient plasticity can phenomenologically capture the increased dislocation density due to gradients in plastic strain near the crack tip and the associated local strengthening. We aim at: (i) understanding the nature of the associated crack tip stress elevation, and (ii) assessing the influence of strain gradients in crack growth resistance. Thus, we first examine analytically the asymptotic nature of crack tip fields. Our findings, corroborated by finite element analysis, reveal the existence of an inner elastic stress state, reminiscent of a dislocation free zone. Crack growth is then predicted for short and long cracks using a cohesive zone model, and a rational basis is provided for brittle fracture in the presence of plasticity

свернуть