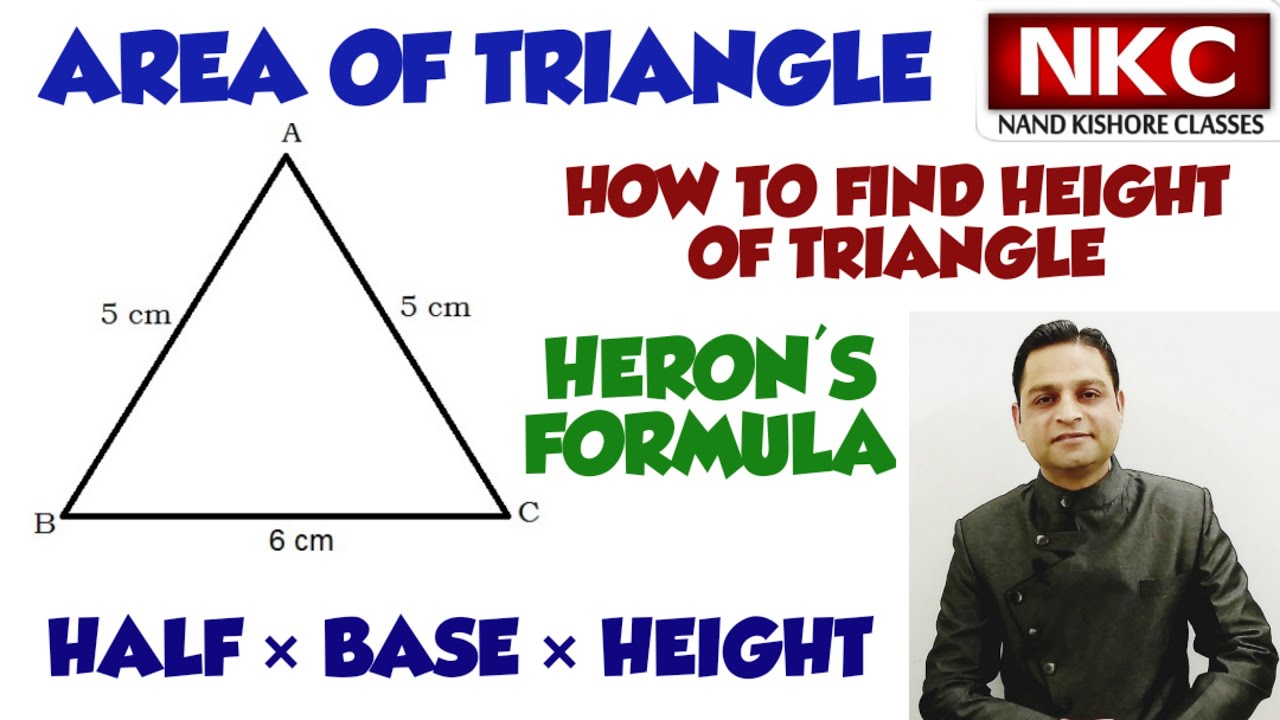
Area of Triangle | Area of Triangle | Find out Height of Triangle | Half x Base x Height | Heron's Formula
One must watch this lecture. This method explained in the video is very helpful for making maths calculation easy specially in competitive exams.
Welcome to Nand Kishore Classes
For 8th, 9th & 10th (Mathematics)
New Batches start w.e.f. 1st April 2021 (Online)
To Fill the Registration Form, Click at below Link
[ Ссылка ]...
Click at below links to download the PDFs containing YouTube Links
1. Basic Math
[ Ссылка ]...
2. Shortcut Tricks & Reasoning
[ Ссылка ]...
3. Kids Activities
[ Ссылка ]...
4. Class 4th
[ Ссылка ]...
5. Class 5th
[ Ссылка ]...
6. Class 8th
[ Ссылка ]...
7. Class 9th
[ Ссылка ]...
8. Class 10th
[ Ссылка ]...
9. Class 11th
[ Ссылка ]...
10. Class 12th
[ Ссылка ]......
Half x base x height
Two Methods to find out Area of Triangle | Half x Base x Height | Heron's Formula
Area of a Triangle from Sides
You can calculate the area of a triangle if you know the lengths of all three sides, using a formula that has been known for nearly 2000 years.
It is called "Heron's Formula" after Hero of Alexandria (see below)
Just use this two step process:
Step 1: Calculate "s" (half of the triangles perimeter):
s = a+b+c 2
Step 2: Then calculate the Area:
herons formula A = sqrt( s(s-a)(s-b)(s-c) )
Example: What is the area of a triangle where every side is 5 long?
Heron's formula, also known as Hero's formula, is the formula to calculate triangle area given three triangle sides. It was first mentioned in Heron's book Metrica, written in ca. 60 AD, which was the collection of formulas for various objects surfaces and volumes calculation. The basic formulation is:
area = √(s * (s - a) * (s - b) * (s - c))
where s is the semiperimeter - half of triangle perimeter:
s = (a + b + c) / 2
However, other forms of this formula exist - if you don't want to calculate the semi perimeter by hand, you can use the formula with side lengths only:
area = 0.25 * √((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c))
Heron's formula proof
There are many ways to prove the Heron's area formula, but you need to know some geometry basics. You can use:
Algebra and the Pythagorean theorem;
Trigonometry and the law of cosines.
Other proofs also exist, but they are more complex or they use the laws which are not so popular (such as e.g. a trigonometric proof using the law of cotangents).
Algebraic proof
Triangle with sides a,b,c, height from right angle h, dividing hypotenuse c to segments d and c-d
In this proof, we need to use the formula for the area of a triangle:
area = (c * h) / 2
All the values in the formula should be expressed in terms of the triangle sides: c is a side so it meets the condition, but we don't know much about our height. So to derive the Heron's formula proof we need to find the h in terms of the sides.
From the Pythagorean theorem we know that:
h² + (c - d)² = a² and h² + d² = b², according to the figure above
Subtracting those two equations gives us:
c² - 2 * c * d = a² - b² from which you can derive the formula for d in terms of the sides of the triangle:
d = (-a² + b² + c²) / (2 * c)
Next step is to find the height in terms of triangle sides. Use the Pythagorean theorem again:
h² = b² - d²
h² = b² - ((-a² + b² + c²) / (2 * c))² - it's already in terms of the sides, but let's try to reduce it to nicer form, applying the difference of squares identity:
h² = ((2 * b * c) - a² + b² + c²) * ((2 * b * c) - a² + b² + c²) / (4 * c⁴)
h² = ((b + c)² - a²) * (a² - (b - c)²) / (4 * c²)
h² = (b + c - a) * (b + c + a) * (a + b - c) * (a - b + c) / (4 * c²)
Apply this formula to first equation, the one for triangle area:
area = (c * h) / 2 = 0.5 * c * h
area = 0.5 * c * √((b + c - a) * (b + c + a) * (a + b - c) * (a - b + c) / (4 * c²))
area = 0.25 * √((b + c - a) * (b + c + a) * (a + b - c) * (a - b + c)
Here you are! That's the Heron's area proof. Changing the final equation into the form using semiperimeter is a trivial task.
Trigonometric proof
Triangle ABC with sides a,b,c and angles α β γ
Have a look at the picture - a, b, c are the sides of the triangle and α, β, γ are the angles opposing these sides. To find the proof of Heron's formula with trigonometry, we need to use another triangle area formula - given two sides and angle between them:
area = 0.5 * a * b * sin(γ)
Welcome to Nand Kishore Classes
Facebook Page -
[ Ссылка ]...
YouTube Channel -
[ Ссылка ]...
Instagram -
[ Ссылка ]...
Twitter -
[ Ссылка ]
Website
[ Ссылка ]