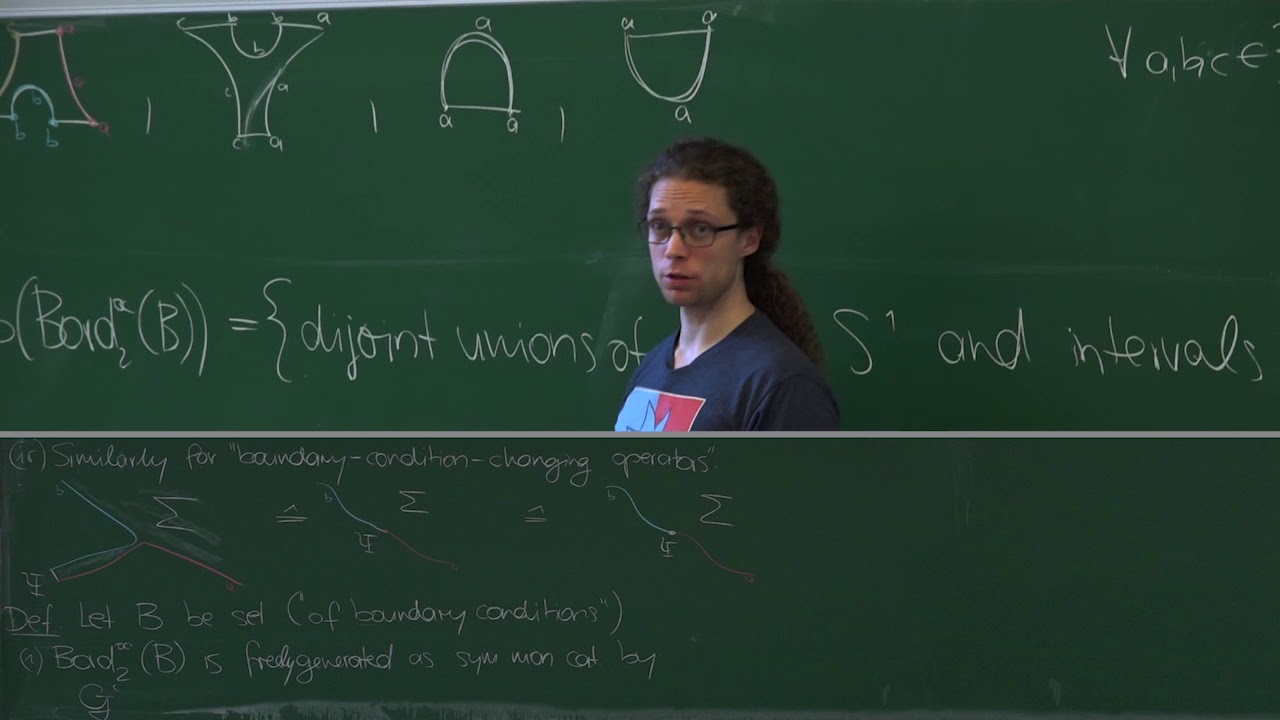These lectures aim to be a gentle introduction to the algebraic and categorical description of boundaries and defects in 2d rational conformal field theories. Much of the time will in fact be spent on topological field theories, where it is easier to see e.g. how boundary conditions are naturally organised in terms of categories. We will introduce and discuss this algebraic language in general, and illustrate it with standard examples like state sum models and sigma models. Finally we will outline how rational CFTs are described in terms of certain tensor categories (such as representations of vertex algebras) and certain algebraic data in them (roughly: the choice of modular invariant partition function), and illustrate everything with an example such as su(2)_k.
======
1. Lead 00:00:00
2. Boundary condition changing operators 00:00:10
3. Generators of the Bordism category 00:04:22
4. Functor on the open and closed bordisms 00:19:56
5. Theorem by Lazaroiu, Moore-Segal and Lauda-Pfeiffer 00:27:44
6. Examples 00:38:22
7. Questions from the audience 00:42:50