A talk by Erik Demaine presented live at the 23rd Thailand-Japan Conference on Discrete and Computational Geometry, Graphs, and Games [[ Ссылка ]] on September 3, 2021.
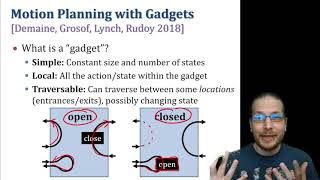
Abstract: Most motion planning problems — designing the route for one or more agents (robots, humans, cars, drones, etc.) through a changeable environment — are computationally difficult: NP-hard, PSPACE-hard, or worse. Such hardness proofs usually consist of several "gadgets" — local pieces of environment with limited agent interactions/traversals, some of which change local state, which in turn change available interactions/traversals — that can be pasted together into the overall reduction. In this talk, I'll describe our quest to characterize exactly which such gadgets suffice to prove different kinds of hardness, in our "motion-planning-through-gadgets" framework that has developed over the past few years. This theory enables many hardness proofs, old and new, to be distilled down to a single diagram of a single gadget.
To learn more, check out the following papers/theses:
[ Ссылка ]
[ Ссылка ]
[ Ссылка ]
[ Ссылка ]
[ Ссылка ]
[ Ссылка ]